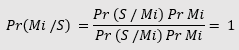Este texto es un extracto del libro ‘Ciencias Formales y Filosofía‘ y contiene fórmulas que fueron adaptadas al presente formato (Descargar PDF del extracto o PDF del libro completo)
El sentido de esta presentación es explicar por qué la figura de Rolando Chuaqui influyó y sigue influyendo de manera estable en académicos e intelectuales de tan diferentes orígenes y formaciones. Obviamente ello ayudará a explicar también por qué las Jornadas que llevan su nombre, así como lo esperamos lo sea la publicación que el lector tiene ahora en sus manos, se han convertido en un producto estable y duradero de este influjo. Es entendible que dicha influencia, innegablemente extraña al medio nacional chileno, sea en parte el resultado natural de los muchos talentos intelectuales que adornaban a Chuaqui, pero pensamos que aun más decisiva que ellos era la singular personalidad que sirvió de suelo para que tales talentos fructificaran. La personalidad de Chuaqui era a su vez compleja y profunda como sencilla y directa. Esto significa que Chuaqui aunaba en su personalidad tendencias, si no contradictorias, al menos antagónicas. Sin embargo, es justo decir que su vida, en su dimensión personal y académica, es tal vez el mejor ejemplo que conocemos de cómo tales tendencias pueden resolverse fluidamente en una armónica unidad. Dado el contexto en que se inserta esta presentación, hablaremos aquí fundamentalmente de cómo se gestó en el plano académico aquella unidad y cómo se expresó tanto en su formación, sus investigaciones y su enseñanza.
En su formación académica vemos de inmediato dos tendencias aparentemente opuestas: por una parte, eligió estudiar medicina en la Universidad de Chile, una disciplina eminentemente práctica, y por otra, casi inmediatamente se sintió interesado por cuestiones teóricas vinculadas a la disciplina, por ejemplo, acerca de los fundamentos lógicos y metodológicos de las ciencias médicas. La forma que Chuaqui ideó para resolver esta dualidad (y superar de paso algunos aspectos particularmente complejos para él de la práctica médica, p.ej. la práctica quirúrgica) fue trasladarse a USA e ingresar al grupo de Lógica y Metodología de la Ciencia de la Universidad de California-Berkeley, programa interdisciplinario de los departamentos de matemáticas y filosofía de dicha universidad. Al regresar a Chile, en vez de asociarse a una facultad de medicina y después de un breve paso por la Facultad de Ciencias de la Universidad de Chile, se integra finalmente en la Pontificia Universidad Católica de Chile donde iniciaría una intensa actividad en pro del desarrollo de las ciencias exactas, particularmente la matemática, llegando con el tiempo a ser el primer Decano de la Facultad de Matemáticas, que él ayudó a crear. Sin embargo, esta decisión a favor de una disciplina muy alejada de la medicina no significó en la vida de Chuaqui un abandono definitivo de esta última pues la formación adquirida le permitió seguir reflexionando profundamente sobre sus fundamentos y sus aplicaciones. Aun más, Chuaqui llegó a convencerse de que era fundamental tender puentes reflexivos permanentes entre las diferentes disciplinas científicas y sus respectivas prácticas. En una clase magistral dictada en 1992 en la Facultad de Humanidades de la Universidad de Santiago titulada “Disciplina e interdisciplina” él hizo perfectamente clara esta convicción. Decía, “[es] mi convencimiento que para hacer estudios interdisciplinarios serios hay que partir de una disciplina estudiada, también, muy seriamente. Creo que, en general, la manera normal de llegar a la interdisciplina es a través de la profundización de la disciplina misma. Todo está unido con todo: al estudiar matemática profundamente, por ejemplo, se llega a la filosofía, como yo, o a la historia, a aun al arte, como otros”. Y él ejemplificaba esta convicción con su propio caso agregando adicionalmente “como muchos d
e ustedes saben, yo estudié primero medicina. Con el título de médico, fui admitido al Programa de Lógica y Metodología de las Ciencias, un programa interdisciplinario entre matemáticas y filosofía de la Universidad de California en Berkeley. Así, sin tener estudios formales de las disciplinas del programa mismo fui admitido a él (aunque solo condicionalmente al principio)”. A continuación, él se explayó acerca de dos ejemplos de actividad interdisciplinaria en los que estuvo intensamente involucrado como matemático, médico y filósofo: en primer lugar, los fundamentos de la probabilidad y la estadística, y, en segundo, los fundamentos de la ciencia cognitiva y la inteligencia artificial. Casi al finalizar su clase magistral y especulando acerca de la conexión entre filosofía, ciencia y tecnología, él concluía diciendo “me parece que la separación entre una investigación pura y aplicada es muy nociva para el desarrollo. Hay un continuo […], entre la investigación más pura y las aplicaciones más concretas. Quebrar este continuo es artificial y creo que perjudicial […]. Aun más, yo creo que no debe haber separación entre filosofía y otras ciencias humanas, ciencia básica y tecnología”. Esto sugiere que Chuaqui tenía clara conciencia de la necesidad de buscar síntesis productivas -de conectar todo con todo- a través de la reflexión profunda acerca de los fundamentos de cada ciencia. Esta fue la solución que él encontró para resolver los antagonismos que enfrentó en su propio camino intelectual y la que siguió luego aplicando consecuentemente.
En sus investigaciones, como ya se observa de acuerdo con lo dicho anteriormente, Chuaqui buscó la misma integración. Ello no solo se refleja en las palabras citadas anteriormente sino directamente en sus áreas de intereses. Por una parte, investigó en áreas tan abstractas como el análisis no estándar, la teoría impredicativa de las clases y los fundamentos de la probabilidad. Y, sin embargo, vio en todas ellas posibilidades de investigación aplicada. La forma que ideó para capturar sus relaciones entre los más abstracto de su producción y sus eventuales aplicaciones fue de nuevo original y penetrante. Daremos aquí solo un ejemplo relacionado con su obra más ambiciosa Truth, Possibility and Probability; New Logical Foundations of Probability and Statistical Inference. Este libro propone en lo general una interpretación novedosa de la probabilidad basada en los conceptos de posibilidad y verdad lógica, que explica tanto los usos epistémicos como los usos en teorías científicas de la probabilidad y captura las intuiciones originales de los fundadores del cálculo de probabilidades. En esta obra se encuentran variados ejemplos de aplicación, sobre todo relacionados con la teoría de la decisión en el ámbito de la medicina y el derecho. Sin embargo, junto con aplicaciones directas de su formalismo, Chuaqui brinda ejemplos informales de aplicación, que siguieren cómo dicho formalismo puede servir para zanjar cuestiones prácticas fundamentales. El ejemolo que consideremos aquí discute la forma en que dos principios probabilísticos defendidos extensamente por Chuaqui, el principio de Inferencia Directa (PID) y el de Inferencia Inversa (PII), subyacen en los modelos de diagnóstico médico de una enfermedad. PID dice, formulado de la manera más sencilla posible, que podemos inferir, a partir de la creencia de una persona p en el tiempo t que la probabilidad aleatoria de un suceso A es r, que el grado racional de la creencia de p en A (i.e la probabilidad epistémica de A) también es r. Por contraste a PID, que nos lleva a aceptar las hipótesis propuestas, PII es un principio de inferencia que permite rechazar hipótesis. Formulado igualmente de manera simplificada, PII dice que, dado un dispositivo aleatorio (un conjunto de resultados posibles) que debemos explicar y un conjunto alternativo de hipótesis epistémicamente posibles (un modelo en la terminología de Chuaqui) para ese propósito, rechazaremos una hipótesis K del último conjunto si hay un experimento discriminados E para K que tiene un resultado α tal que la probabilidad de a es baja o algo peor en relación con K. Para entender completamente PII – un genuino aporte metodológico de Chuaqui – deberíamos también especificar las definiciones de algunas nociones involucradas en la definición anterior como son las de resultado peor, experimento discriminador y regla ideal de rechazo, entre otras. Ya que no podemos hacer esto en esta breve presentación, nos limitaremos a continuación a comentar su ejemplo y las consecuencias prácticas que de él se derivan.
Si admitimos que cada enfermedad tiene una causa que produce diferentes racimos de síntomas entonces, según Chuaqui, la primera implica un dispositivo aleatorio que determina los racimos posibles de síntomas que se presentan en diferentes personas. Así concebidas, las enfermedades se pueden interpretar como procesos estocásticos que evolucionan en el tiempo. A su vez, en una persona dada, los cambios evolutivos de la enfermedad se manifiestan como deferentes racimos de síntomas. Lo original de esta visión es lo que llamaríamos filosóficamente, su modelismo. Es decir, Chuaqui concibe la naturaleza de la conexión entre las diferentes alteraciones corporales producto de la evolución en el tiempo de la enfermedad como posibilística, en el sentido que las alteraciones en un cuerpo tiempo determinan las posibilidades de alteración en los tiempos sucesivos (y sus probabilidades asociadas). Por otra parte, la relación entre las alteraciones y los síntomas también puede interpretarse modalmente, es decir, ciertas alteraciones determinan un rango de racimos posibles de síntomas (con sus respectivas probabilidades) y no un racimo específico. De esto se desprende que Chuaqui acepta cierto realismo o primitivismo causal: él cree que existen procesos causales reales (los que producen las alteraciones corporales) y por tanto que existe cierto orden causal subyacente. Es este orden el que permite determinar (y descartar) posibilidades sucesivas en el tiempo y con ello asignar probabilidades. DE ahí que su causalismo sea probabilístico solo en un sentido derivado (esto seguramente afectará también la concepción general de indeterminismo que defendía Chuaqui pues, al menos, lo atenuará). A continuación, Chuaqui considera un modelo bayesiano, Chuaqui arriba a la conclusión que dicho modelo enfrenta dificultades de adecuación que llevarán a cometer serios errores de diagnóstico, siendo la dificultad más grave el hecho que el modelo asume que los síntomas solo pueden dar evidencia para una categoría de enfermedades, pero no para una enfermedad particular sufrida por un sujeto particular. Frente a esto, Chuaqui recomienda utilizar su PII (aunque sin abandonar PID, o sea, sin abandonar la regla bayesiana) para hacer diagnóstico. Es decir, en este caso, asumimos que existen hipótesis alternativas para la explicación de los síntomas del paciente, donde cada hipótesis exige que el paciente tenga una enfermedad particular o una combinación de enfermedades. Por lo tanto, el paciente no es escogido a partir de un conjunto de pacientes, sino que es considerado individualmente. Ahora bien, al comparar, en un caso más realista, ambos modelos se ve la plausibilidad de Chuaqui. Si suponemos que existe un solo síntoma S que presenta en una enfermedad (Mi) y que ha sido observado (lo que llamaríamos en medicina, un síntoma patognomónico), entonces en el modelo bayesiano tenemos que Pr(S/ Mi) = 0 para todo j≠i¹. Usando la regla bayesiana obtenemos
Como se esperaría. Sin embargo, esto bloquea pensar en la enfermedad desde un punto de vista evolutivo, es decir, no podemos aplicar de nuevo el modelo bayesiano pues él nos obliga a aceptar la enfermedad dado que está tiene probabilidad uno. Empero, cambios debido a la observación de otros síntomas no previamente detectados, como es obvio, aún siguen siendo lógicamente posibles, lo que podría consecuentemente alterar el diagnóstico. El modelo de Chuaqui permite tal posibilidad. Aplicando PII al mismo caso (y desconsiderando los detalles) obtenemos Prd[E=S] = 0 para todo j≠i*. Inicialmente, ya que todos los síntomas peores que S para Mj toman probabilidad cero, la probabilidad del rechazo de Mi es cero y por tanto debe ser aceptada. Sin embargo, si suponemos que otros síntomas aparecen, aunque el rechazo de Mi sea muy improbable, se puede plantear finalmente su rechazo. Pero, en este caso, esto significaría que cualquier Mj debería permanecer rechazada. En tal caso el modelo de Chuaqui permite considerar dos opciones: o que las alternativas consideradas no son exhaustivas o el rechazo ya sea de la nueva evidencia o (tal vez lo mas sensato) del síntoma patognomónico. La posibilidad de considerar siempre estas alternativas le da obviamente al modelo de Chuaqui una eficacia práctica y una plausibilidad de las cuales no puede gozar el modelo bayesiano. Este ejemplo hace claro, por tanto, que ni siquiera en sus trabajos más abstractos Chuaqui se apartó del ideal de la síntesis y de la conexión con los asuntos humanos más urgentes.
Finalmente, en su labor educativa, como pueden atestiguar todos los que trabajamos cerca de Chuaqui, esta actitud de integración era aun más palpable pues, como él indicaba explícitamente en el discurso citado al comienzo, la encarnaba en el aula al conectar la matemática con la filosofía. Por ejemplo, sus investigaciones en fundamentos de la matemática lo llevaron a la filosofía de la matemática, y de allí a la filosofía de la ciencia, y de ahí a la filosofía en general. Esto lo convirtió en un insistente defensor y difusor del platonismo matemático contemporáneo. Además, se interesó crecientemente por las interpretaciones modelo-teoréticas de la estructura de las teorías científicas en la línea de Sneed, Balzer y Moulines, cuando la discusión sobre estas materias en las aulas filosóficas chilenas simplemente no existía. Desde una posición filosófica más general, consumió una parte importante de sus esfuerzos teóricos intentando convencernos, en el aula y fuera de ella, que el escepticismo (en cualquier de sus formas) era inviable. Él sostenía que la única manera de garantizar la objetividad o la intersubjetividad del conocimiento era no intentar ninguna justificación de él. Cualquiera de estas justificaciones debía finalizar, a su juicio, en idealismos o cuasi-idealismos y por tanto se convertirían en víctimas potenciales de la voracidad del escéptico. Finalmente, como los que lo conocen intuían, esta última convicción filosófica estaba, al menos, sugerentemente conectada con sus convicciones religiosas, pues, como creyente comprometido, él se sentía próximo a cierta forma de fideísmo de acuerdo a la cual toda necesidad de justificación de la verdad revelada pierde sentido. Ahora se puede adivinar entonces cómo y con qué intensidad Chuaqui vivía el desiderátum de la integración y la unidad de conocimientos.
Por otra parte, esta actitud de integración entraba en armonioso acuerdo con su actitud general ante la vida y las personas: su tolerancia, sencillez, su paciencia y sobre todo su generosidad eran sin duda los más persuasivos y cálidos instrumentos de difusión de sus profundas y muchas veces áridas convicciones intelectuales. Déjesenos decir que en esto la comparación con Carnap es casi inevitable y para nada exagerada. Como Carnap, la tolerancia y generosidad atravesaban tanto su vida personal como su vida intelectual y le daban un sello propio a su relación con los demás, fuesen colegas, alumnos o simples desconocidos animados por el simple deseo de saber. Y como Popper recuerda de Carnap también, Chuaqui vivía igual que el segundo en una quieta pero absorta devoción a los problemas teóricos, de la cual solo lo sacaba su intenso deseo de escuchar críticas y observaciones.
Hay un célebre dictum atribuido al filósofo norteamericano Donald Davidson que dice: “es difícil incrementar la pasión sin disminuir la verdad”. Sin embargo, este dictum no puede ser verdadero al menos de Chuaqui pues de la manera que él escogió vivir su propio dictum – que todo está conectado con todo-, la pasión fue un vehículo para la búsqueda de la verdad y viceversa. Esperemos por ello que esta publicación y las venideras atestigüen que Chuaqui estuvo entre nosotros para enseñarnos que ambas, la pasión y la verdad, forman el continuo elemental sobre el cual toda vida intelectual adquiere su grandeza y su último sentido.
Prof. Wilfredo Quezada²
Prof. Renato Lewin³
¹Prd(S) es la probabilidad del síntoma S en el paciente que tiene la enfermedad M y, por lo tanto, es distinta de Pr(S/M), ya que no tenemos ninguna distribución común de probabilidad para todas las enfermedades. PrD(S) corresponde al concepto de likelihood matemática de Fischer.
²Profesor Jornada Completa, Departamento de Filosofía de la Universidad de Santiago de Chile. Doctor (PhD) en Filosofía por el King’s College de la U. de Londres. Miembro del comité organizador de las Jornadas Rolando Chuaqui K.
³Profesor Titular Adjunto, Departamento de Matemáticas de la Pontificia Universidad Católica de Chile. Doctor (Phd) en Matemáticas por la Univesity of Colorado-boulder en USA. Amigo personal de Rolando Chuaqui Kettlun.